Data Operations

Plots in Tecplot 360 rely on the datasets attached to each frame. You can modify, create, transform, interpolate, duplicate, and delete the data in the current dataset using the Data menu. You can also use the data operation capabilities of Tecplot 360 to create plots of analytical functions. By using layout files, macros, and/or equation files, you can create complex data operations that can be repeated on different datasets.

Changes to the dataset within Tecplot 360 do not affect the original data file(s). You can save the modified data by choosing Write Data from the File menu. When you save a layout file, a journal of data operations is saved and those operations are repeated when the layout file is read at a later time. If the data in the file has changed, or the data file is overwritten with new data, the operations are applied to the new data. Alternatively, any datasets that have been modified are also saved to data files (see Layout Files and Layout Package Files for details).

Data Alteration through Equations

Use Data→Alter→Specify Equations (or click the 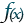toolbar equation toolbar button) to alter data in existing zones. The dialog allows you to change the values of entire variables or specific data points. You can also use this dialog to create new variables.

Changes made to the dataset in the Specify Equations dialog are not made to the original data file. You can save the changes by saving a layout file or writing the new data to a file. Saving a layout file will keep your data file in its original state, but use journaled commands to reapply the equations.

Variables defined in your data file, or variables you create yourself, are referenced in equations by surrounding them with curly braces, like {RPM}. This syntax must be used even when first defining a variable, for example {RPM} = {RPS} * 60 to define a new RPM variable from an existing RPS variable. Variable and function names provided by Tecplot 360 do not require the braces.
specify equations

The Specify Equations dialog has the following options and fields:

Equation(s)

Enter the equation(s) using the syntax described in Equation Syntax.

Data Set Info

Opens the Data Set Info dialog (see Data Set Information).

Ignore divide by zero errors

When activated, suppresses the error dialog and returns the largest or smallest possible value depending on the sign of the dividend when a divide by zero condition occurs. 0/0 will return 0.

Save Equations

Save all equations in the Equation(s) field to a text file with an .eqn format.

Load Equations

Load an equation file previously saved.

Zones to Alter

Select which zones to alter. You can manually select the zones in the list (holding Shift when clicking to create a range, or Control to toggle individual zones on or off). You may use the buttons below the list to select all zones, all active zones, or no zones.

When creating a new variable, if all zones are not selected, Tecplot will create a passive variable as a placeholder for any zones that are not included in the data alteration since all zones in a dataset must have the same number of variables. Passive variables effectively return zero for every point or cell value, do not consume any memory, and can be replaced at any time with other data alterations.
Index Ranges

Select the index ranges to alter in the selected zones. You may skip this step if you want to apply the equation to all points of the selected zones. Use the special value 0 or Mx to specify the maximum index. You can also use the values Mx-1 (to specify the index one less than the maximum index), Mx-2, and so forth.

For Ordered Data, the I-Index, J-Index, and K-index options correspond to the I, J, and K values in the dataset. For finite element data, the I-Index corresponds to the range of nodes and the J-Index corresponds to the cell-centered values. The K-index has no bearing on finite element data.

The Skip field indicates the increment between indices. 1 means apply the calculation to every data point, 2 means to every other data point, 3 to every third point, and so on. When creating a new variable, the new variable’s value is set to zero at any index value that is skipped.

New Var Data Type

(if applicable) - Select the data type of the new variable. The following data types are available:

Auto

Tecplot 360 assigns the data type based upon the variables used in the right-hand side of the equation.

Single

Four-byte floating point values.

Double

Eight-byte floating point values.

Long Int

Four-byte integer values.

Short Int

Two-byte integer values.

Byte

One-byte unsigned integer values (can contain values from zero to 255).

Bit

Either zero or one.

New Var Location

(if applicable) - Select the location of the new variable. The options are:

Auto

(default) - "Auto" is set to node unless all variables in the equation are located at the cell center.

Node

Stores variable with nodal information. (see Indexing Nodal Ordered Data).

Cell-Center

Stores variable with nodal information. (see Indexing Cell-centered Ordered Data).

Compute

Click the Compute button to alter the data. If an error occurs during the alteration (because of division by zero, overflow, underflow, etc.), an error message is displayed, all of the zones are restored to their previous state as of the beginning of processing that equation, and processing stops. The results of equations that have been successfully processed, however, are retained.

For example, if you enter three equations, and the second contains an error, the final state is the result of processing only the first equation. The second equation is rolled back due to the error, and the third is not processed at all.

Every time you hit the [Compute] button, the equations are calculated. Be sure to remove previously computed equations before computing new ones.

Equation Syntax

You can enter multiple equations in the Equation(s) text field of the Specify Equations dialog. Each equation occupies one line of the text field as demarcated by the Enter key (not necessarily by where they wrap in the text field). The equations are applied in order to all specified zones and data points.

Tecplot 360 equations have the following form:

LValue = F(RValue1, RValue2, RValue3,…​)

Where:

F() - A mathematical expression.

LValue - An existing or new variable.

RValueN - A value (such as a constant, variable value, or index value).

If LValue already exists in the dataset of the active frame, the equation is used to modify that variable. (The same variable may be used on the right side of the equation to refer to the pre-calculation value and thereby modify it based on its original value.) If the variable does not already exist, the equation is used to create a new variable as a function of existing variables.

There may be any number of spaces within the equation. However, there cannot be any spaces between the letters of intrinsic-function names nor in variables referred to by name. (See Equation Operators and Functions.)

Equation Variables and Values

A variable is specified in one of the following ways:

Its order in the data file

A variable may be referenced according to its order in the data file, where V1 is the first variable in the data file, V2 is the second, and so forth.

To create a new variable using this specification, you must specify the number of the next available variable (i.e. if there are 5 variables in the dataset), the new variable must be called V6. You will receive an error message, if you attempt to assign an invalid variable number.

You can confirm the number and order of variables in the data file in the Data Set Information dialog (choose Data→Data Set Info). The variables in the dataset are listed on the right-hand side of the page.
By its name

To reference a variable by its name, enclose the name with curly braces ({ and }). For example, to set V3 equal to the value of the variable named R/RFR, you can enter:

V3 = {R/RFR}

Variable names are not case sensitive. Leading and trailing spaces are also not considered. However, spaces within the variable name are significant.

If two or more variables have the same name, the first variable is used when the variable is referred to by name. So, if both V5 and V9 are named R/rfr, V5 is used.

The curly braces can also be used on the left-hand side of the equation. In this case, if a variable with that name does not exist, a new variable is created with that name for all zones.

By a letter code

Variables and index values may be referenced by the following letter codes:

I

Depends on the data type and the new variable’s ‘New Var Location’ value:

  • Ordered data:

    • If ‘New Var Location’ is set to ‘Node’, I is the I index number of a node.

    • If ‘New Var Location’ is set to ‘Cell center’, I is the lowest I index associated with the cell.

  • FE data:

    • If ‘New Var Location’ is set to ‘Node’, I is the node index number.

    • If ‘New Var Location’ is set to ‘Cell center’, I is 1.

J

Depends on the data type and the new variable’s ‘New Var Location’ value:

  • Ordered data:

    • If ‘New Var Location’ is set to ‘Node’, J is the J index number of a node.

    • If ‘New Var Location’ is set to ‘Cell center’, J is the lowest J index associated with the cell.

  • FE data:

    • If ‘New Var Location’ is set to ‘Node’, J is 1.

    • If ‘New Var Location’ is set to ‘Cell center’, J is the element number.

K

Depends on the data type and the new variable’s ‘New Var Location’ value:

  • Ordered data:

    • If ‘New Var Location’ is set to ‘Node’, K is the K index number of a node.

    • If ‘New Var Location’ is set to ‘Cell center’, K is the lowest K index associated with the cell.

  • FE data:

    • If ‘New Var Location’ is set to ‘Node’, K is 1.

    • If ‘New Var Location’ is set to ‘Cell center’, K is 1.

X

The variable assigned to the X-axis. In XY-plots, all active mappings must have the same X-variable in order for this variable name to be valid.

Y

The variable assigned to the Y-axis. In XY-plots, all active mappings must have the same Y-variable in order for this variable name to be valid.

Z

The variable assigned to the Z-axis (if in 3D Cartesian).

A

The variable assigned to the Theta-axis for Polar plots. For this variable to be valid, the plot type must be set to Polar Line. In addition, all active mappings must have the same Theta-variable.

R

The variable assigned to the R-axis for Polar plots. The plot type must be Polar Line, and all active mappings must have the same R-variable for this variable name to be valid.

U

The X-component of vectors (if defined).

V

The Y-component of vectors (if defined).

W

The Z-component of vectors (if defined).

B

The value-blanking variable for the first active constraint (if applicable).

C

The contour variable for contour group 1 (if defined in the Contour Details dialog).

S

The scatter-sizing variable (if defined in the Scatter Size/Font dialog).

SOLUTIONTIME

The current solution time.

ZONENUM

The current zone number.

Letter codes may be used anywhere on the right-hand side of the equation. Do not enclose them in curly braces.

Those letter codes representing variables (all letter codes except I, J, and K) may be used on the left-hand side of the equation as well.

The variables referenced by the letter codes are for the current frame.

Equation Operators and Functions

Binary Operators

In an equation, the valid binary operators are as follows:

+

Addition

-

Subtraction

*

Multiplication

/

Division

**

Exponentiation

Binary operators have the following precedence:

**

Highest precedence

*,/

+,-

Lowest precedence

Operators are evaluated from left to right within a precedence level.

Functions

The following functions are available. Arguments may be variables, constants, expressions, other functions.

SIN(X)

Sine of X (must be specified in radians)

COS(X)

Cosine of X (must be specified in radians)

TAN(X)

Tangent of X (must be specified in radians)

ABS(X)

Absolute value of X

ASIN(X)

Arcsine of X (result given in radians)

ACOS(X)

Arccosine of X (result given in radians)

ATAN(X)

Arctangent of X (result given in radians)

ATAN2(A,B)

Arctangent of A/B (result given in radians)

SQRT(X)

Returns the positive square root of X

LOG(X), ALOG(X)

Natural logarithm (base e) of X. Both forms are equivalent.

LOG10(X), ALOG10(X)

Logarithm base 10 of X. Both forms are equivalent.

EXP(X)

Exponentiation (base e); EXP(X)=

MIN(A, B)

Minimum of A or B

MAX(A, B)

Maximum of A or B

SIGN(X)

Returns -1 if X is negative, +1 otherwise

ROUND(X)

Round X to the nearest integer

TRUNC(X)

Remove fractional part of X

RAND(N)

Returns random number between 1 and N inclusive, different for each element in the variable

Conditional Expressions

Conditional expressions may be written using the IF function.

IF(P,T,F)

If the predicate expression P is true (has a non-zero value), returns the value of expression T, otherwise returns the value of expression F. Both T and F are fully evaluated regardless of the value of P; there is no "short-circuiting."

The predicate expression may include comparison and Boolean operators, as summarized in the following table.

Operator Description Example

==

Equal To

{A} = IF(X==2.0, 3, 4) assigns to variable A: 3 if X equals 2.0, otherwise 4

!=

Not Equal To

{A} = IF(X != Y,Z,2) assigns to variable A: Z if X does not equal Y, otherwise 2

>

Greater Than

{A} = IF(X > 1.0, 4, 5) assigns to variable A: 4 if X > 1.0, otherwise 5

>=

Greater Than or Equal To

{A} = IF(X >= Y, 4, Z) assigns to variable A: 4 if X >= Y, otherwise Z

<

Less Than

{A} = IF(X < Y, 4, Z) assigns to variable A: 4 if X < Y otherwise Z

<=

Less Than or Equal To

{A} = IF(X <= Y, 4, Z) assigns to variable A: 4 if X <= Y, otherwise Z

&&

Logical AND

{A} = IF(X < Y && X > 3, 8,9) assigns to variable A: 8 if X < Y AND X > 3, otherwise 9

||

Logical OR

{A} = IF(X == 2 || X > 3, 5,6) assigns to variable A: 5 if X == 2 OR X > 3, otherwise 6

These operators are valid only within the first argument of an IF function. They may not be used elsewhere in an expression. For example, {A} = X > 1 is invalid. Instead, use {A} = IF(X > 1, 1, 0) or similar.

Python-style operator chaining (such as A < B < C) is not supported. Although this construction is syntactically valid, it will not produce the expected result. Use A < B && B < C instead.

&& has a higher precedence than (will be evaluated before) ||. When in doubt, use parentheses.

Derivative and Difference Functions

The derivative functions can be called in the same manner as intrinsic functions. Derivative and difference functions can be calculated with respect to the following variables:

Variable Definition Restricted to:

x, y, z

variable assigned to the x-axis, y-axis or z-axis, respectively

XY Line[1], or 3D

a

variable assigned to the theta-axis

Polar Line

r

variable assigned to the radial-axis

Polar Line

i, j, k

index range

Ordered Zones

The complete set of first and second-derivative and difference functions are listed below:

Type Function Calls Applicable Variables

First Order

ddx, ddy, ddz, dda, ddr

x, y, z, a, or r

Second Order

d2dx2, d2dy2, d2dz2, d2da2, d2dr2

x, y, z, a or r

Second-Order (cross derivatives)

d2dxy, d2dyz, d2dxz, d2dar

xy, yz, xz, or ar

The derivative function ddx is used to calculate ; d2dx2 calculates .

Type

Function Calls

Applicable Variables

First Order

ddi, ddj, ddk

i, j, or k

Second Order

d2di2 d2dj2, d2dk2

i, j, or k

Second Order (cross derivatives)

d2dij, d2djk, d2dik

ij, jk, or ik

The difference functions ddi, d2di2, and so forth, calculate centered differences of their argument with respect to the indices I, J, and K based on the indices of the point. For example:

For ordered zones, spatial derivative functions are calculated using the chain rule with difference functions. For example:

or:

The spatial derivatives of indices, such as ddx(i), are calculated from their inverses, such as ddi(x), using standard curvilinear coordinate transformations.

For finite-element zones, spatial derivatives are calculated using the Moving Least-Squares technique. The variable at a particular node or cell center is assumed to vary quadratically in space about that point, and least-squares is used with all nodes surrounding the point to fit a polynomial function, whose coefficients then become the first and second derivatives of the variable.

Boundary Values

Boundary values for first-derivative and difference functions (ddx, ddy, ddz, ddi, ddj, and ddk) of ordered zones are evaluated in one of two methods: simple (default) or complex [2]

For simple boundary conditions, the boundary derivative is determined by the one-sided first derivative at the boundary. This is the same as assuming that the first derivative is constant across the boundary (i.e., the second derivative is equal to zero).

For complex boundary conditions, the boundary derivative is extrapolated linearly from the derivatives at neighboring interior points. This is the same as assuming that the second derivative is constant across the boundary (i.e. the first derivative varies linearly across the boundary).

For second-derivatives and differences (d2dx2, d2dy2, d2dz2, d2dxy, d2dyz, d2dxz, d2di2, d2dj2, d2dij, d2dk2, d2djk, and d2dik), these boundary conditions are ignored. The boundary derivative is set equal to the derivative that is one index in from the boundary. This is the same as assuming that the second derivative is constant across the boundary.

You can create your own derivative boundary conditions by using the index range and the indices options discussed previously.

The use of derivative and difference functions is restricted as follows:

  • Derivatives and differences for IJK-ordered zones are calculated for the full 3D volume. The IJK-mode for such zones is not considered.

  • If the derivative cannot be defined at every data point in all the selected zones, the operation is not performed for any data point.

  • Derivative functions are calculated using the active frame’s axis assignments. Be careful if you have multiple frames with different variable assignments for the same dataset.

  • Derivatives at the boundary of two zones may differ since Tecplot 360 operates on only one zone at a time while generating derivatives.

Integration

Use the Analyze menu to calculate integrals with Tecplot 360. See Performing Integrations for information.

Auxiliary Data

You may use auxiliary data containing numerical constants in equations. The syntax for using auxiliary data in equations is:

AUXZONE[nnz]:Name
AUXDATASET:Name
AUXFRAME:Name
AUXVAR[nnv]:Name
AUXLINEMAP[nnm]:Name

Where:

nnz = the zone number(s)
nnv = the variable number(s)
nnm = the line map number(s)
Name = name of the auxiliary data

For example, a dataset auxiliary data constant called Pref would be referenced using AUXDATASET:Pref. Equations using this auxiliary data might appear as:

{P} = {P_NonDim} * AUXDataSet:Pref

Zone Number Specification

By following a variable reference with square brackets ([ and ]), you can specify a specific zone from which to get the variable value.

The zone number must be a positive integer constant less than or equal to the number of zones. The zone specified must have the same structure (I, IJ, or IJK-ordered or finite element) and dimensions (IMax, number of nodes) as the zone(s) the equation(s) will be applied to.

If you do not specify a zone, the zone modified by the left-hand side of the equation is used.

Zone specification works only on the right-hand side of the equation.

Index Specification

By following a variable reference with parentheses, you can specify indices for ordered data only. Indices can be absolute or an offset from the current index.

Index offsets are specified by using the appropriate index i, j or k followed by a + or - and then an integer constant. Any integer offsets may be used. If the offset moves beyond the end of the zone, the boundary value is used. For example, V3(i+2) uses the value V3(IMAX) when I=IMax-1 and I=IMax. V3(I-2) uses the value of V3(1) when I=1 or I=2.

Absolute indices are specified by using a positive integer constant only. For example, V3(2) references V3 at index 2, regardless of the current i index.

If the indices are not specified, the current index values are used.

Variable Sharing Between Zones

For zones with the same structure and index ranges, you can set a variable to be shared by specifying that the variable for those zones have the values from one zone. For example, if zones 3 and 4 have the same structure and you compute V3=V3[3] for zones 3 and 4, V3 will be shared.

Subsequent alteration of the variables may result in loss of sharing.

Equation Restrictions

The zone and index restrictions specified in the Specify Equations dialog can be overridden on an equation by equation basis. To specify restrictions for a single equation add the colon character (:) at the end of the equation followed by one or more of the following:

Equation Restrictor Comments

<Z=<set>>

Restrict the zones.

<I=start[,end[,skip]]>

Restrict the I-range.

<J=start[,end[,skip]]>

Restrict the J-range.

<K=start[,end[,skip]]>

Restrict the K-range.

<D=datatype>

Set the data type for the variable on the left hand side. This only applies if a new variable is being created.

<V=valuelocation>

Set the value location (NODAL or CELLCENTERED) for the variable on the left hand side. Only applicable if a new variable is being created.

For example, to add one to X in zones 1, 3, 4, and 5:

X=X+1:<Z=[1,3-5]>

The following example adds one to X for every other I-index. Note that zero represents the maximum index.

X=X+1:<I=1,0,2>

The next example creates a new variable of type Byte:

{NewV}=X-Y:<D=Byte>

Macros and Equations

Tecplot 360 allows you to put your equations in macros. A macro with just equations in it may be referred to as an equation file, and in fact equation files saved using the Save Equations button are macro files with an .eqn extension. An equation in a macro file is specified using the $!ALTERDATA macro command. Equation files may also include comment lines and must start with the comment #!MC 1410, like other macro files. If you are performing complex operations on your data, and/or the operations are repeated frequently, equation files can be very helpful.

You can create equation files from scratch using an ASCII text editor, or you can create your equations interactively by using the Specify Equations dialog and then save the resulting equations. The standard file name extension for equation files is .eqn.

For example, you might define an equation to compute the magnitude of a 3D vector. In the Specify Equations dialog, it would have the following form:

{Mag} = sqrt(U*U + V*V + W*W)

In a macro file, it would have the following form:

#!MC 1410
$!ALTERDATA
EQUATION = "{Mag} = sqrt(U*U + V*V + W*W)"

The interactive form of the equation must be enclosed in double quotes and supplied as a value to the EQUATION parameter of the $!ALTERDATA macro command.

To read an equation file, select Load Equations on the Specify Equations dialog. In the Load Equation File dialog, select an equation file that contains a set of equations to apply to the selected zones of your data. The equations in the equation file will be added to the list of equations in the dialog. All equations are applied to your data when you click Compute.

Equations in equation files may be calculated somewhat differently depending on whether the computation is done from within the Specify Equations dialog or by running the equation file as a macro. When loaded into the Specify Equations dialog, equations that do not contain zone or index restrictions use the current zone and index restrictions shown in the dialog. When processed as a macro file, the equations apply to all zones and data points. To include zone and index restrictions, you must include them in the equation file as part of the $!ALTERDATA command.

Refer to the Scripting Guide for more information on working with the $!ALTERDATA command.

Equation Examples

In the following equation, V1 (the first variable defined in the data file) is replaced by two and a half times the existing value of V1:

V1 = 2.5*V1

The following equation sets the value of a variable called Density to 205. A new variable is created if a variable called Density does not exist.

{Density} = 205

In the next equation, the values for Y (the variable assigned to the Y-axis) are replaced by the negative of the square of the values of X (the variable assigned to the X-axis):

Y = -X**2

The following equation replaces the values of V3 with the values of V2 rounded off to the nearest integer. A new variable is created if there are only two variables currently in the data set.

V3 = round(V2)

In the following equation, the values of the fourth variable in the data set are replaced by the log (base 10) of the values of the third variable.

V4 = ALOG10(V3)

Suppose that the third and fourth variables are the X and Y-components of velocity and that there are currently a total of five variables. The following examples create a new variable (V6) that is the magnitude of the components of velocity.

V6 = (V3*V3+V4*V4)**0.5

or

V6 = sqrt(V3**2+V4**2)

You can also accomplish the above operation with the following equation (assuming you have already defined the vector components for the active frame):

{Mag} = sqrt(U*U + V*V)

The following equation sets the value of a variable named diff to the truncated value of a variable named depth subtracted from the existing value of depth:

{diff} = {depth} - trunc({depth})

In the next equation, C (the contour variable) is set to the absolute value of S (the scatter-sizing variable), assuming both C and S are defined:

C = abs(S)

In the following example, a new variable is created (assuming that only seven variables initially existed in the data file). The value for V8 (the new variable) is calculated from a function of the existing variables:

V8 = SQRT((V1*V1+V2*V2+V3*V3)/(287.0*V4*V6))

The above operation could have been performed in two simpler steps as follows:

V8 = V1*V1+V2*V2+V3*V3
V8 = SQRT(V8/(287.0*V4*V6))

The following equation replaces any value of a variable called TIME that is below 5.0 with 5.0. In other words, the values of TIME are replaced with the maximum of the current value of TIME and 5.0:

{TIME} = max({TIME},5)

The following equation creates variable V4 which has values of X at points where X<0; at other points, it has a value of zero (this does not affect any values of X):

V4 = min(X,0)

Another example using intrinsic functions is shown below:

V8 = 55.0*SIN(V3*3.14/180.0) + ALOG(V4**3/(v1+1.0))

You can also reference the I, J, and K-indices in an equation. For example, if you wanted to cut out a section of a zone using value blanking, you could create a new variable that is a function of the I and J-indices (for IJ-ordered data). Then, by using value-blanking, you could remove certain cells where the value of the value-blanking variable was less than or equal to the value blanking cut-off value.

Here is an example for calculating a value-blanking variable that is zero in a block of cells from I=10 to 30, and is equal to one in the other cells:

V3 = min((max(I,30)-min(I,10)-20),1)

The following equation replaces all values of Y with the difference between the current value of Y and the value of Y in zone 1. (If zone 1 is used for the data alteration, the new values of Y will be zero throughout that zone.)

Y = Y - Y[1]

The following equation replaces the values of V3 (in an IJ-ordered zone) with the average of the values of V3 at the four adjacent data points:

V3 = (V3(i+1,j)+V3(i-1,j)+V3(i,j+1)+V3(i,j-1))/4

The following equation sets the values of a variable called TEMP to the product of the values of a variable called T measured in four places: in zone 1 at two index values before the current data point, in the current zone at an absolute index of three, in zone 4 at the current data point, and in the current zone at the current data point.

{TEMP} = {T}[1](i-2) * {T}(3) * {T}[4] * {T}

Indices may be combined with zone specifications. The zone is listed first, then the index offset. For example:

V3 = V3 - V3[1](i+1)
Y = Y[1] - Y[2](1) + Y(1,j+3) + Y

Referencing variables by letter code:

V3 = I + J
V4 = cos(X) * cos(Y) * cos(Z)
{Dist} = sqrt(U*U + V*V + W*W)
{temp} = min(B,1)

Specifying the Zone number for a given variable:

V3 = V3 - V3[1]
X = ( X[1] + X[2] + X[3] ) / 3
{TempAdj} = {Temp}[7] - {Adj}
V8 = V1[19] - 2*C[21] + {R/T}[18]

Data Smoothing

You can smooth the values of a variable of any zone (2D or 3D) or 1D line map (plotted in either XY or Polar) to reduce "noise" and lessen discontinuities in data.

Smoothing can be used after inverse-distance interpolation to reduce the artificial peaks and plateaus this type of interpolation can produce. Each pass of smoothing shifts the value of a variable at a data point towards an average of the values at its neighboring data points.

Zones must be mesh-based to be smoothed. If your data consists of disconnected points, see Inverse-Distance Interpoation and Irregular Data Point Triangulation for possible approaches to converting it to a form suitable for use with the Tecplot 360 smoothing feature.

To smooth data in Tecplot 360, select Alter→Smooth from the Data menu.

smooth

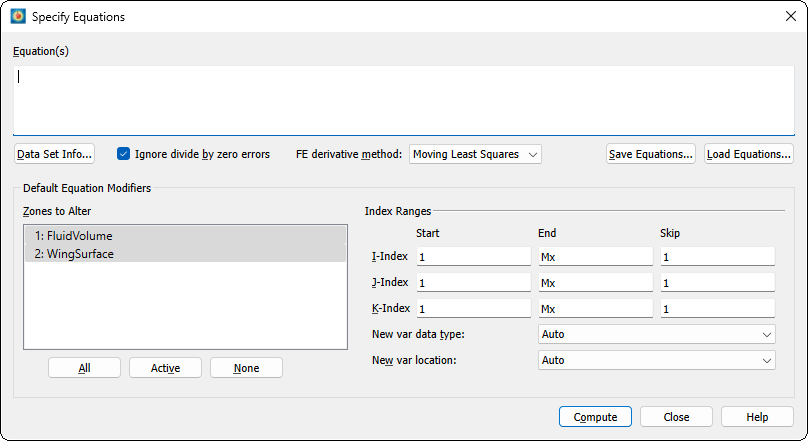
The Smooth dialog has the following options:

Zone

Specify the zone to smooth from the Zone drop-down. The zone should not intersect itself.

For a given plot type, the dimension of the zone must be less than or equal to the dimension of the plot type. That is, in 3D Cartesian plots, volume, surface and line zones may be smoothed, while in 2D Cartesian plots, volume zones cannot be smoothed.

Variable

Select the variable to smooth. For line plots, the variable must be a dependent variable for an active mapping for that zone.

Number of Passes

Specify the number of smoothing passes to perform. The default is 1. A greater number of passes results in greater smoothing, but takes more time.

Coefficient

Specify the relaxation factor for each pass of smoothing. Enter a number between zero and one (exclusively). Large numbers flatten peaks and noise quickly. Small numbers smooth less each pass, rounding out peaks and valleys rather than eliminating them.

Boundary

Select the boundary conditions by which to smooth from the Boundary drop-down.

Fixed

The points at the boundary are not changed in value. For finite element data, only fixed boundary conditions may be used.

First Order

The points at the boundary are smoothed based on the assumption that the first derivative normal to the boundary is constant. This will tend to cause contour lines of the smoothed variable to be perpendicular to the boundary.

Second Order

The points at the boundary are smoothed based on the assumption that the second derivative normal to the boundary is constant. This option may overextrapolate derivatives at the boundary.

Smooth

Click to perform smoothing. While the smoothing is underway, the progress is displayed in the status bar. A Stop button displayed in the status bar allows you to interrupt the operation.

Smoothing Method

Tecplot 360 uses the Jacobi method with the Coefficient used as a relaxation factor (always < 1, so it’s under-relaxed). For ordered zones, Tecplot 360 does this in generalized curvilinear coordinates, which has the effect of length- (or area- or volume-) weighting a node’s neighboring values. For the fixed boundary condition, boundary values remain unchanged. For first-order boundaries, the boundary values are relaxed toward the neighboring interior values, and for second-order boundaries, they are relaxed toward a constant slope (zero curvature) relative to the two neighboring interior points. For finite-element zones, Tecplot 360 relaxes each value toward the inverse-distance weighted average of its neighbors. Only the fixed boundary condition is available for FE zones.

Limitations of Smoothing

  • Finite element zones cannot be smoothed with anything other than Fixed boundary conditions.

  • Tecplot 360 uses the active frame’s axis assignments to determine the variables to use for the coordinates in the smoothing, and also to determine whether the smoothing should be done with XY Line, Polar, and 2D or 3D Cartesian plot types. Be sure to select the correct frame if you have multiple frames with different variable assignments for the same dataset.

  • Any axis scaling is ignored while smoothing.

  • For I-ordered or finite element line segment zones, the active frame can be in the XY Line, or 3D Cartesian plot types. In XY Line, the variable must be the dependent variable of one active mapping for that zone.

  • For IJ-ordered, finite element triangle, or finite element quadrilateral zones, the active frame can be a 2D or 3D Cartesian plot type, but you cannot smooth the variables assigned to the X and Y-axes in Cartesian.

  • For IJK-ordered, finite element tetrahedral, or finite element brick zones, the plot type must be 3D Cartesian, and you cannot smooth the variables assigned to the X, Y, and Z-axes. The IJK-mode is ignored. The zone is smoothed with respect to the entire 3D volume.

  • Smoothing does not extend across zone boundaries. If you use a boundary condition option other than Fixed (such that values along the zone boundary change), contour lines can be discontinuous at the zone boundaries.

  • Smoothing is performed on all nodes of a zone, and disregards value blanking.

Fourier Transform

The Fourier transform feature (Data→Fourier Transform) allows you to transform one-dimensional ordered linear data into the frequency domain. One or more dependent variables in the data set are taken to be a representation of some function of a single independent variable, such as time, and this function is decomposed into its constituent sine waves. Variables are added to the data set to indicate these waves' frequency in Hertz, phase, and amplitude in each selected zone, and an XY of the resulting amplitudes is created in a new frame.

The dependent variables for a Fourier transform must be single-valued. The independent variable domain need not be constantly spaced; data will be resampled linearly if necessary.

The resulting frequency, amplitude, and phase variables (three for each dependent variable) are stored in Fourier transform result zones, one for each source zone. The result zones are given the name "Fourier Transform" followed by text indicating the source zone, independent variable, and window function used to calculate them. Result zones are assigned new time strands using the same groupings as the source zones if they belong to time stands; otherwise the resulting zones are static.

The result variables in the result zone are given the names Frequency, Amplitude and Phase followed by text indicating the dependent variable involved in the calculation. If the independent variable is non-uniform, Frequency is a uniform interpolation of the original data.

Newly-created zones are assigned passive variables for all variables that previously existed in the dataset, and all previously-existing zones are assigned passive variables for all new variables created by the Fourier transform.

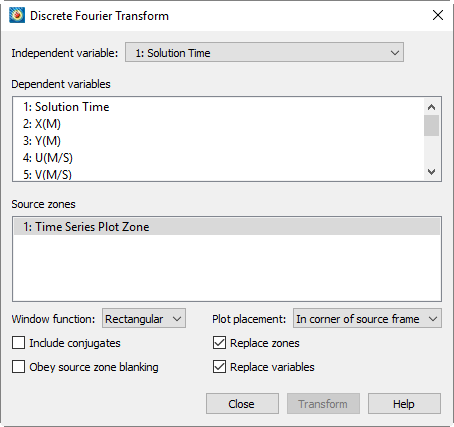
fourier
Independent Variable

The variable used as the frequency domain. If this variable’s spacing is non-uniform, this variable is used in conjunction with each dependent variable for interpolation to create a uniform frequency for the Fourier transform.

Dependent Variables

Choose the dependent variables to be transformed. Each will appear on the resulting XY plot as its own linemap.

Source Zones

Choose the zones for which the transform should be calculated.

Window Function

A function applied to the dependent variables before performing the transform (but after interpolation) to taper the data. Rectangular, triangular, Hann, and Hamming filters are provided.

Plot Placement

Where to initially place the result plot of the transform showing the distribution of frequencies in the data. The plot can be moved and resized as desired afterward.

In corner of source frame

A new frame is created for the frequency plot in the upper right corner of the frame containing the data being transformed.

Tile with existing frames

All frames, including the new one, are adjusted to the same size and arranged on the paper in a grid.

Include Conjugates

For purely real numbers, fully half of the results of the Fourier transform are conjugates (values with the same real part but opposite imaginary parts, which behave identically in situations where a real number is required). Toggling-off this option will allow the transform to be performed approximately twice as fast. as only one conjugate is calculated.

Obey Source Zone Blanking

If value blanking is active and this option is toggled-on, value blanking is applied to the values of both independent and dependent variables before interpolation is performed. If data values eliminated by blanking cause the data to be non-uniform, the values are interpolated appropriately. All blanked data values up to the first non-blanked value, and all blanked data values after the last non-blanked value, are ignored, providing a way to constrain the domain of the transform.

Replace Zones/Variables by Name

If either or both are toggled-on, the results of the transform are stored in existing result zones and/or variables, based on their names, if such zones and/or variables exist. Otherwise, new result zones and/or variables are created.

You may also access this feature by right-clicking a line map and choosing Fourier Transform from the context menu. In this case, the line map you click defines the independent and dependent variable used. All other settings are taken from last values entered in the dialog; the dialog does not appear.

Axial Rotation

The Axial Rotation dialog, available from the Alter submenu of the Data menu, allows you to rotate one or more 2D or 3D zones using the right-hand rule. The variables rotated are the spatial variables (X, Y, and, for 3D zones, Z) and the vector variables assigned using Plot → Vector → Variables. For 3D zones, you may also choose the axis of rotation.

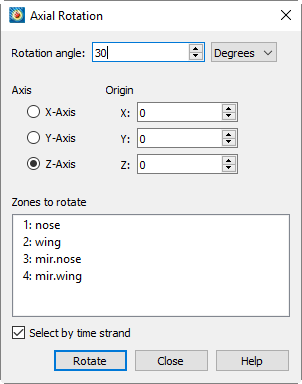
axial rotation

The Axial Rotation dialog has the following options:

Rotation Angle

The angle by which the data should be rotated. May be specified in degrees or radians using the drop-down menu to the right of the entry field.

Axis

For 3D zones, choose the axis around which rotation should occur. Not available for 2D zones, which are always rotated about a notional axis perpendicular to the zone.

Origin

For rotation around a point other than (0, 0) or (0, 0, 0), enter the location of the origin using the X, Y, and (for 3D zones) Z fields.

Zones to Rotate

Click, Control-click, and/or Shift-click in the zone list to select one or more zones.

Select by Time Strand For transient data, if this checkbox is toggled on, the zones in the Zones to Rotate list are grouped by time strand, so that selecting a zone selects all the zones in that time strand.

Using a macro, it is possible to rotate around arbitrary axes rather than just X, Y, and Z, and to specify exactly which variables, if any, should be rotated as spatial variables and which as vector variables, including no spatial variables at all, or multiple vector variables. See $!ROTATEDATA in the Scripting Guide.

Zone Creation

The Create Zone submenu of the Data menu allows you to add data to your plot. The menu has the following options:

Rectangular Zone Creation

Creating a rectangular zone is often the first step in interpolating irregular data into an ordered grid

Tecplot 360 allows you to create a new ordered rectangular zone with the dimensions in the I, J and K-directions you specify. This is done either with the Create Rectangular Zone tool (only) or the Create Rectangular Zone dialog. The zone that you create has the same number of variables as other zones in the dataset.

To create a rectangular zone, select Create Zone→Rectangular from the Data menu.

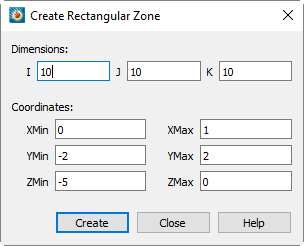
create rectangular zone

The Create Rectangular Zone dialog has the following options:

Dimensions

Enter the number of data points in the I, J and K-directions.

  • To create an I-ordered zone, enter 1 for both the J and K-dimensions.

  • To create an IJ-ordered zone, enter 1 for the K-dimension. The z-axis variable will equal ZMin throughout the created zone.

  • To create an IJK-ordered zone, enter a K-dimension greater than one.

Coordinates

Enter the start and end points of the physical coordinates (X,Y and Z).

Create

Select the [Create] button to create the zone.

Tecplot 360 uniformly distributes the data points in the I, J and K directions. Any variable not assigned to an axis is set to zero.

By using the Specify Equations dialog under the Data→Alter menu, you can modify the X, Y, and Z-coordinates, and the values of the other variables as well, by using equations or Equation files. See Data Alteration through Equations.

Circular or Cylindrical Zone Creation

Tecplot 360 allows you to create a new ordered circular or cylindrical zone with the dimensions in the I, J, and K-directions you specify. The I-dimension determines the number of points on each radius of the zones. The J-dimension determines the number of points around the circumference. The K-dimension determines the number of layers in the zone, creating a cylinder.

You create a circular or cylindrical zone with the Create Circular Zone dialog (accessed via Data→Create Zone, or with the Create Circular Zone tool (only). The zone that you create has the same number of variables as other zones in the dataset.

If you have no current dataset, Tecplot 360 creates one with two or three variables, depending on the K-dimension. If you specify K=1, the dataset is created as IJ-ordered, and has two variables. If you specify K > 1, the dataset is created as IJK-ordered, and has three variables.

To create a circular zone select Create Zone→Circular from the Data menu.

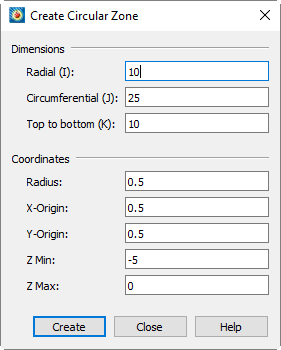
create circular zone

The Create Circular Zone dialog has the following options:

Dimensions

Enter the dimensions of your circular zone:

Radial (I)

Specify the number of points the radial direction (I)

Circumferential (J)

Specify the number of points in the circumferential direction (J)

Top to Bottom (K)

Specify the number of points for the height of the cylinder (K). Set K equal to one to create a circular zone.

Coordinates

Radius

Enter the length of the radius.

X-Origin and Y-Origin

Enter the coordinates for the zone center

ZMin and ZMax

Enter the minimum and maximum Z-coordinates. For a circular zone (where K=1), the Z variable is set to ZMin for all points.

Create

Select the Create button to create the zone.

For IJ-ordered, Tecplot 360 creates a zone in which I-circles are connected by J-radial lines. For 3D (K→1), Tecplot 360 creates a K-layered cylindrical zone having I-circles connected by J-radial planes. All other variables are set to zero These two scenarios are shown below

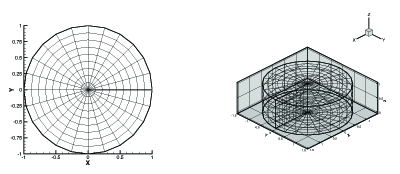
circular zone combo

Using the Alter option from the Data menu, you can modify the X-, Y-, and Z-coordinates, and the values of the other variables as well, by using equations or equation files. See Data Alteration through Equations.

Zone Duplication

To create a full duplicate of one or more existing zones, select Create Zone→Duplicate from the Data menu. In the Create Duplicate Zone dialog, select the source zone(s). Each duplicate zone has the same name as its source zone.

create duplicate zone
After a zone is duplicated, all variables in the newly created zone(s) will be shared with their corresponding source zone(s).

Mirror Zone Creation

To create a duplicate zone that is the mirror image of an existing zone, select Create Zone→Mirror from the Data menu.

You can only create mirrored zones along one of the standard axes (2D) or the plane determined by any two axes (3D).

The Create Mirror Zone dialog has the following options:

create mirror zone
Source Zone(s)

Select the Sources Zone(s).

Mirror Axis

Specify the axis () or axis plane (3D) to mirror about.

Create

Select the [Create] button to create the zone.

Each mirror zone has a name of the form "Mirror of zone sourcezone", where sourcezone is the number of the zone from which the mirrored zone was created.

The variables in the newly created zone(s) are shared with their corresponding source zone(s), except for the coordinate and velocity normal to the symmetry plane.

Axial Duplication

The Axial Duplication dialog, available from the Create Zone submenu of the Data menu, allows you to create sucessively-rotated duplicates of one or more 2D or 3D zones using the right-hand rule. For example, if your data set contains a simulation of one blade of a turbine, and there are thirty blades in the full turbine, you can create 29 duplicates, each rotated twelve degrees from the previous, to be able to visualize the entire turbine.

The variables rotated are the spatial variables (X, Y, and, for 3D zones, Z) and the vector variables assigned using Plot → Vector → Variables. For 3D zones, you may also choose the axis of rotation. Streamtraces are not duplicated; place streamtraces after zone duplication.

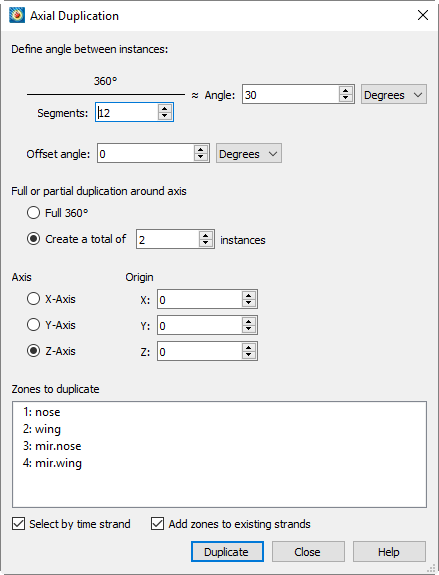
axial duplication

The Axial Duplication dialog has the following options:

Define Angle Between Instances

Contains two interdependent fields, Angle and Segments, which are used to specify how many duplicates are in a full 360° rotation of the zone.

The number of segments is determined by dividing the angle into 360,° and the angle is calculated by dividing the number of segments into 360°. Editing one automatically updates the other. You may choose to specify (or calculate) the angle in ethier degrees or radians.

Offset Angle

The additional amount by which the first duplicate should be rotated; may be specified in degrees or radians. For example, if you specify an angle between instances of 20° and an offset of 40°, the first duplicate will be made at 60°, the second at 80°, the third at 100°, and so on.

This field may be used, for instance, when you have already created some duplicates and want to create additional duplicates that do not overlap the ones you have already created. In the example just given of angle 20° and offset 40°, perhaps you have already created two duplicates (at 20'° and 40°) and wish to create additional duplicates. In this case, offset of 40° specifies that the last existing duplicate is at 40° and that new duplicates should be created in the next "slot" beyond that, at 60°.

Full or Partial Duplication

Choose to create as many new zones as are necessary for a full rotation by choosing Full 360° (this will result in the number of duplicates entered or calculated in the Define Angle Between Instances, less the original zone(s) being duplicated) or create a specified number of rotated duplicates.

Axis

For 3D zones, choose the axis around which rotation should occur. Not available for 2D zones, which are always rotated about a notional axis perpendicular to the zone.

Origin

For rotation around a point other than (0, 0) or (0, 0, 0), enter the location of the origin using the X, Y, and (for 3D zones) Z fields.

Zones to Duplicate

Click, Control-click, and/or Shift-click in the zone list to select one or more zones.

Select by Time Strand

For transient data, if this checkbox is toggled on, the zones in the Zones to Duplicate list are grouped by time strand, so that selecting a zone selects all the zones in that time strand

Add Zones to Existing Strands

For transient data, adds the duplicate zones to the same time strand as the original zones if toggled on. Otherwise, the duplicate zones are assigned new strand IDs if the soruce zones belonged to strands, otherwise they are made static.

Using a macro, it is possible to rotate around arbitrary axes rather than just X, Y, and Z, and to specify exactly which variables, if any, should be rotated as spatial variables and which as vector variables, including no spatial variables at all, or multiple vector variables. See $!AXIALDUPLICATE in the Scripting Guide.

Data Extraction from an Existing Zone

You may create new zones by extracting (or interpolating) data from existing zones in a number of ways. Derived objects, such as contour lines, FE-boundaries, iso-surfaces, slices, or streamtraces may be extracted to be independent zones. You may also extract data using a specified slice plane, discrete points, points from a polyline, or points from a geometry.

The procedures for extracting derived objects are discussed in the chapters related to those objects. For details see Contour Layer, Streamtrace Extraction as Zones, and Iso-Surface Extraction. Extracting slices, both derived and arbitrarily defined, is described in Extracting Slices to Zones.

Subzone Extraction

To create a subzone of an existing ordered zone, select Extract→Subzone from the Data menu.

Subzone extraction is available for ordered zones only.

The Extract Subzone dialog has the following options:

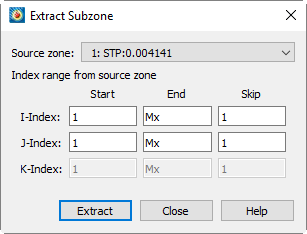
extract subzone
Source Zone

Select the source zone (ordered zones only).

Index Range from Source Zone

Specify the desired subzone as a range of I, J, and K-indices. You may use the special value 0 or Mx to indicate the maximum of that index, and the values Mx-1 to represent one index less than the maximum, Mx-2 for two less than the maximum, and so forth.

Extract

Select the Extract button to create the zone. Each extracted subzone is given the name "Subzone."

Data Point Extraction

You may create an I-ordered zone by extracting data points from the current dataset along a polyline that lies within the edges of a zone with connectivity. To extract points along a polyline:

  1. If necessary, create the polyline geometry using the toolbar insert polyline 1056 polyline tool. Click each of the points in the polyline, then double-click the last point (or press Escape) to finish the polyline. You may also extract points along an already-existing polyline.

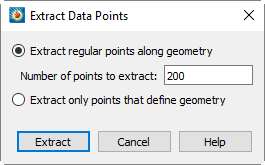
  2. Right-click the polyline geometry in the workspace and choose Extract Points from the context menu to open the Extract Data Points dialog.

    extract data points

  3. Use the Extract Data Points dialog to control how data points are extracted. The dialog has the following options:

    Extract regular points along geometry

    Select this option to extract the specified number of points distributed uniformly along the geometry.

    Number of points to extract

    Enter the number of points to extract. This field is available only if you are extracting regular points along a geometry.

    Extract only points which define geometry

    Select this option to extract only the endpoints of the segments in the geometry.

    Any necessary interpolation is performed using the same method used in probing. The spatial interpolation method is piecewise-linear by default. Cells are, in effect, divided by adding nodes at their center and face centers, until all cell pieces are tetrahedral. The extra nodes are calculated by arithmetically averaging the variable values at all nodes (for the cell-center node) or all face nodes (for the face-center nodes). Within each of these sub-cells, variables are interpolated linearly.

    From triangular faces, linear interpolation is used to determine the value of the extracted points. On quadrilateral faces, a point of the center of mass of the quadrilateral is created and assigned a value equal to the average of the four corners. The surface is then broken down into four triangles using this center point and the four corners, and the extracted point value is interpolated linearly on the face of the triangle that surrounds it.

    If a surface utilizes cell-centered values, the nodal values at the corners are interpolated, then the extracted points are interpolated from those nodal values.

    Volume interpolation, piece-wise by default, calculates to first-order accuracy. For second-order accuracy (tri-linear interpolation), add the following line to your tecplot.cfg file:

    $!INTERFACE DATA {VOLUMECELLINTEROPLATIONMODE = TRILINEAR}

  4. If you created a new polyline for the extraction operation, you may wish to delete it by again right-clicking it, then choosing Delete from the context menu.

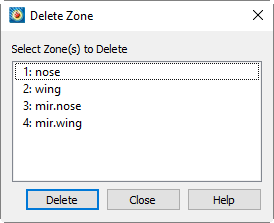
Zone Deletion

In any dataset with more than one zone, you can delete any unwanted zones. To delete a zone, select Delete→Zone from the Data menu. You cannot delete all zones; if you attempt to delete all zones, the lowest numbered zone is not deleted.

delete zone

Variable Deletion

To delete a variable, select Delete→Variable from the Data menu. The Delete Variable dialog is shown below.

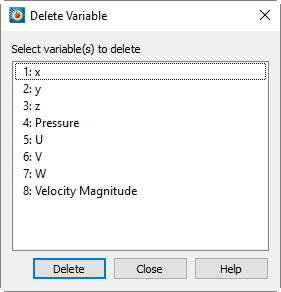
delete variable

When deleting a variable, keep in mind that deleting a variable removes it from all zones. You cannot delete a variable used in a Calculate-on-demand function. See Calculate-on-demand Variables.

Data Interpolation

In Tecplot 360, interpolation refers to assigning new values for the variables at data points in a zone based on the data point values in another zone (or set of zones).

For example, you may have a set of data points in an I-ordered zone that are distributed randomly in the XY-plane. This type of data is sometimes referred to as unordered, ungridded, or random data. In Tecplot 360, it is referred to as irregular data. Using data in this form, you can create mesh plots and scatter plots, but you cannot create contour plots, light-source shading, or streamtraces.

In Tecplot 360, you can interpolate the irregular I-ordered data onto an IJ-ordered mesh, and then create contour plots and other types of field plots with the interpolated data. You can also interpolate your 3D, I-ordered irregular data into an IJK-ordered zone and create 3D volume plots from the IJK-ordered zone. You can even interpolate to a finite element zone.

The accuracy of the interpolation will depend on your data, the density of the destination grid, how well the grid fits the area of your unorganized zone and the settings used for interpolation.

There are three types of interpolation available:

Linear Interpolation

Interpolate using linear interpolation from a set of finite element, IJ-ordered, or IJK-ordered zones to one zone.

Inverse-Distance Interpoation

Interpolate using an inverse-distance weighting from a set of zones to one zone.

Kriging

Interpolate using Kriging from a set of zones to one zone.

Linear Interpolation

Use the Linear Interpolation dialog to interpolate data from one or more ordered or finite element zones onto a destination zone. Irregular I-ordered data cannot be used for the source zones in linear interpolation; you may be able to first create a finite element zone from an irregular, I-ordered zone by using triangulation. (See Irregular Data Point Triangulation.)

Linear interpolation finds the values in the destination zone based on their location within the cells of the source zones. The value is linearly interpolated to the destination data points using only the data points at the vertices of the cell (or element) in the source zone(s).

To perform linear interpolation:

  1. Read the dataset to be interpolated into Tecplot 360 (the source data).

  2. Read in or create the zone onto which the data is to be interpolated (the destination zone).

  3. From the Data menu, choose Interpolate→Linear.

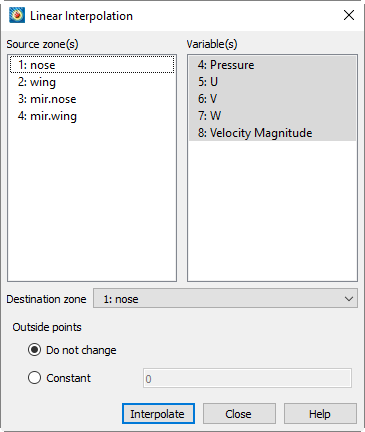
    linear interpolation

  4. From the Linear Interpolation dialog, select the zones to be interpolated from those listed in the Source Zone(s) scrolled list.

  5. Select which variables are to be interpolated from those listed in the Variable(s) scrolled list.

  6. Select the destination zone into which to interpolate. Existing values in the destination zone will be overwritten.

  7. Outside Points - Optionally, choose how to treat points that lie outside the source-zone data field. You have two options:

    • Do Not Change - Preserves the values of points outside the data field. Do Not Change is appropriate in cases where you are using one interpolation algorithm inside the data field, and another outside.

    • Constant - Sets all points outside the data field to a constant value that you specify.

  8. Click the [Interpolate] button to perform the interpolation.

  9. While the interpolation is proceeding, a working dialog appears showing the progress of the interpolation

If you select [Cancel] during the interpolation process, the interpolation is terminated prematurely. The destination zone will be left in an indeterminate state, and you should redo the interpolation.

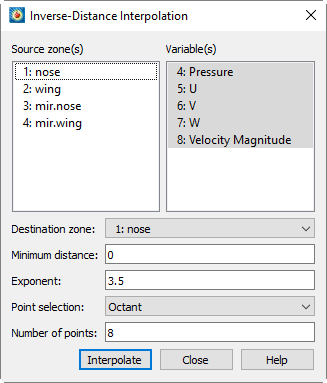
Inverse-Distance Interpoation

Inverse-distance interpolation averages the values at the data points from one set of zones (the source zones) to the data points in another zone (the destination zone). The average is weighted by a function of the distance between each source data point to the destination data point. The closer a source data point is to the destination data point, the greater its value is weighted.

In many cases, the source zone is an irregular dataset—an I-ordered set of data points without any mesh structure (a list of points). Inverse-distance interpolation may be used to create a 3D surface or a 3D volume field plots of irregular data. The destination zone can, for example, be a circular or rectangular zone created within Tecplot 360 Zone Creation).

To perform inverse-distance interpolation in Tecplot 360, use the following steps:

  1. Read the dataset to be interpolated into Tecplot 360 (the source data).

  2. Read in or create the zone onto which the data is to be interpolated (the destination zone).

  3. From the Data menu, choose Interpolate→Inverse Distance.

    inverse distance interpolation

  4. From the Inverse-Distance Interpolation dialog, select the zones to be interpolated from those listed in the Source Zone(s) list.

  5. Select which variables are to be interpolated from those listed in the Variable(s) list.

  6. Select the Destination Zone into which to interpolate. Existing values in the destination zone will be overwritten.

  7. [OPTIONAL] Enter the minimum distance used for the inverse-distance weighting in the Minimum Distance text field. Source data points which are closer to a destination data point than this minimum distance are weighted as if they were at the minimum distance. This tends to reduce the peaking and plateauing of the interpolated data near the source data points.

  8. [OPTIONAL] Enter the exponent for the inverse-distance weighting in the Exponent text field.

    The exponent should be set between 2 and 5. The algorithm is speed-optimized for an exponent of 4, although in many cases, the interpolation looks better with an exponent of 3.5.

  9. [OPTIONAL] Select the method used for determining which source points to consider for each destination point from the Point Selection drop-down. There are three available methods, as follows:

    Nearest N

    For each point in the destination zone, consider only the closest n points to the destination point. These n points can come from any of the source zones. This option may speed up processing if n is significantly smaller than the entire number of source points.

    Octant

    Like Nearest N above, except the n points are selected by coordinate-system octants. The n points are selected so they are distributed as evenly as possible throughout the eight octants. This reduces the chances of using source points which are all on one side of the destination point.

    All

    Consider all points in the source zone(s) for each point in the destination zone.

  10. Click Interpolate to perform the interpolation.

If you select the Cancel button during the interpolation process, the interpolation is terminated prematurely. The destination zone will be left in an indeterminate state, and you should redo the interpolation.

Inverse-distance interpolation ignores the IJK-mode of IJK-ordered zones. All data points in both the source and destination zones are used in the interpolation.

Tecplot 360 uses the active frame’s axis assignments to determine the variables to use for coordinates in interpolation. However, axis scaling is ignored.

The Inverse-Distance Algorithm

The algorithm used for inverse-distance interpolation is simple. The value of a variable at a data point in the destination zone is calculated as a function of the selected data points in the source zone (as defined in the Point Selection drop-down, accessed via Data→Interpolate→Inverse-Distance).

The value at each source zone data point is weighted by the inverse of the distance between the source data point and the destination data point (raised to a power) as shown below:

where and are the values of the variables at the destination point and the source point, respectively, and is the weighting function defined as:

D in the equation above is the distance between the source point and the destination point or the minimum distance specified in the dialog, whichever is greater. E is the exponent specified in the Exponent text field.

Smoothing may improve the data created by inverse-distance interpolation. Smoothing adjusts the values at data points toward the average of the values at neighboring data points, removing peaks, plateaus, and noise from the data. See Data Smoothing for information on smoothing.

Kriging and Inverse Distance Interpolation Improvements
For better results with 3D data, try changing the range of your Z-variable to one similar to the X-range the Y-range. Also, set Zero Value to 0.05.

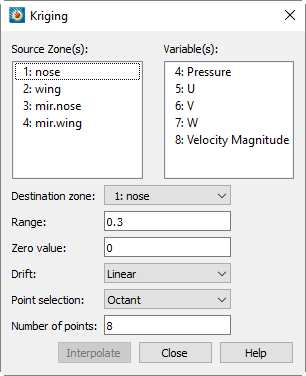
Kriging

Kriging is a more complex form of interpolation than inverse-distance. It generally produces superior results to the inverse-distance algorithm but requires more computer memory and time.

To perform kriging in Tecplot 360, perform the following steps:

  1. Read the dataset to be interpolated into Tecplot 360 (the source data).

  2. Read in or create the zone onto which the data is to be interpolated (the destination zone).

  3. From the Data menu, choose Interpolate→Kriging

    kriging

  4. From the Kriging dialog, select the zones to be interpolated from those listed in the Source Zone(s) scrolled list.

    Tecplot 360 uses the active frame’s axis assignments to determine the variables to use for coordinates in kriging. However, any axis scaling is ignored.

  5. Select which variables are to be interpolated from those listed in the Variable(s) scrolled list.

  6. Select the destination zone into which to interpolate. Existing values in the destination zone will be overwritten.

  7. In the Range text field, optionally enter the distance beyond which source points become insignificant for the kriging. The value is stated as the fraction of the length of the diagonal of the box which contains the data points. A range of zero means that any point not coincident with the destination point is statistically insignificant; a range of one means that every point in the dataset is statistically significant for each point. In general, values between 0.2 and 0.5 should be used.

  8. In the Zero Value text field, optionally enter the semi-variance at each source data point on a normalized scale from zero to one. Semi-variance is the certainty of the value at a data point. A value of zero means that the values at the source points are exact. Greater values mean the values at the source points have some uncertainty or noise. Zero is usually a good number for the zero value, and it causes the interpolated data to fit closely to all the source data points. Increasing the zero value results in smoother interpolated values that fit increasingly more to the average of the source data.

  9. Select the overall trend for the data in the Drift drop-down. This can be Linear (default), None, or Quadratic.

    If the Drift is set to Linear or Quadratic, Tecplot 360 requires that the points selected be non-collinear (non-coplanar in 3D). To avoid this limitation, set Drift to None. Alternatively, you can eliminate coincident points by Irregular Data Point Triangulation before you interpolate.

  10. Select the method used for determining which source points to consider for each destination point from the Point Selection drop-down. There are three available methods, as follows:

    Nearest N

    For each point in the destination zone, consider only the closest n points to the destination point. These n points can come from any of the source zones.

    Octant (default)

    Like Nearest N above, except the n points are selected by coordinate-system octants. The n points are selected so they are distributed as evenly as possible throughout the eight octants. This reduces the chances of using source points which are all on one side of the destination point.

    All

    Consider all points in the source zone(s) for each point in the destination zone. In general, you should not use the All option unless you have very few source points

    The Point Selection option is very important for kriging, because kriging involves the computationally expensive inversion and multiplication of matrices. The computational time and memory requirements increase rapidly as the number of selected source data points increases.

  11. Click Interpolate to begin kriging. While kriging is proceeding, a progress bar appears in the status bar, along with a Stop button that can be clicked to interrupt the operation.

If you interrupt the kriging process, the destination zone is left in an indeterminate state, and you should redo the kriging or delete the destination zone.

The Kriging Algorithm

For a detailed discussion of the kriging algorithm refer to: Davis, J. C., Statistics and Data Analysis in Geology, Second Edition, John Wiley & Sons, New York, 1973, 1986.

Kriging and Inverse Distance Interpolation Improvements#: For better results with 3D data, try changing the range of your Z-variable to one similar to the X-range the Y-range. Also, set Zero Value to 0.05.

Irregular Data Point Triangulation

Triangulation is a process that connects data points to form triangles. You can use triangulation to convert irregular I-ordered datasets into a finite element surface zone. Triangulation is one of the two options for creating field plots from irregular data. The other is interpolation, discussed in Data Interpolation. Triangulation preserves the accuracy of the data by creating a finite element surface zone with the source data points as nodes and a set of triangle elements. Triangulation works best for irregular data.

To triangulate 2D data, make sure your plot is in 2D Cartesian mode and select 2D Triangulation from the Data menu. The 2D Triangulation dialog has the following options:

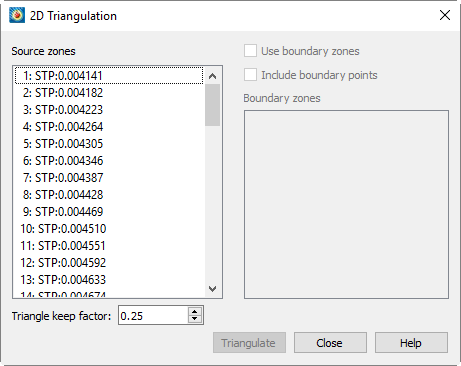
triangulate
Source Zone(s)

Select the zone or zones to triangulate from the list.

Use Boundary Zone(s)

Toggle-on to specify a boundary zone for the triangulation. Select the boundary zone or zones from the list. The boundary zones define the boundaries in the triangulation region. If you do not include boundary zones, Tecplot 360 assumes the data points lie within a convex polygon and that all points in the interior can be connected.

Include Boundary Points

Toggle-on to include the points in the boundary zones in the triangulated zone.

Triangle Keep Factor

This factor is used to define which triangles on the outside of the triangulated zone are "bad" and not included in the triangulation.

At the completion of triangulation, Tecplot 360 attempts to remove bad triangles from the outside of the triangulation. The keep factor is a description of the shape of the triangle between zero (three collinear points) and 1.0 (an equilateral triangle). Typical settings are values between 0.1 and 0.3; settings above 0.5 are not permitted. Bad triangles will not be removed if removing the triangle strands a data point.

Triangulate

Click the Triangulate button to perform the triangulation.

After triangulating your data, you can use the resulting finite element surface zone to create plots. Generally, you turn off the original zone(s) and plot the new zone only, but you can, for example, plot a scatter plot of the original zone(s) along with the contours of the new zone.

Data Spreadsheet

All ordered and finite element data can be viewed using Tecplot 360’s data spreadsheet (accessed via Data→Spreadsheet). The data may be modified within the spreadsheet in order to change the plots Tecplot 360 produces.

Changes to the spreadsheet do not immediately alter the original data file stored on disk. However, saving the plot of altered data as a layout file will save the changes in the data journal. You have the option of overwriting your original data file or creating a new file with the altered data.

The spreadsheet displays Tecplot 360’s data differently depending on the type of zone being examined. An example of the Data Spreadsheet dialog for a finite element zone is shown here; note the X, Y, and Z variables.

data spreadsheet

I-ordered and finite element datasets are displayed with each zone’s variable displayed in a column. IJ-ordered datasets are displayed in the spreadsheet with I along the rows and J along the columns. IJK-ordered datasets are displayed one plane at a time: selecting the K-plane displays I along the rows and J along the columns, selecting the J-plane displays I along the rows and K along the columns, and selecting the I-plane displays J along the rows and K along the columns. With IJK-ordered data, the slice of interest can be selected by entering a specific index or using the up and down arrows provided.

If a variable is not needed in your plot, it may not currently be loaded into memory. In this case, "Not Loaded" is displayed in every cell of that variable’s column. Using the variable in your plot will cause it to be loaded. Click the Load Variables button to open the Load Variable dialog and load any variables you wish to view and edit in the spreadsheet.

To change the data spreadsheet’s display format, select the desired format (Integer, Float, Exponent, or Best Float) from the Format drop-down menu. When Float or Exponent is selected, you may also specify the precision in the Precision field. These options do not affect the actual data, only how it is displayed.

To modify data:

  1. In the Data Spreadsheet dialog, select a zone and variable to modify. Use the menu at the top of the dialog to choose the zone, then find the column representing the desired variable.

  2. If the variable is shared with another zone or zones, the Alter in all Shared Zones toggle is enabled. Select this toggle to keep the variable shared as you modify data, propagating changes to the other zones that share the variable. If this toggle is not selected, the variable will be changed in the selected zone and no longer shared with any other zones. See also Data Sharing.

  3. Select the value of interest from the spreadsheet by finding its row. This will highlight and expand the value to its full precision.

  4. To replace the highlighted value, simply enter the new value. The value is instantly replaced with the new digits entered.

  5. To modify only a few digits from a highlighted value, double-click the cell to switch to edit mode. Click again or use the arrow keys to position the edit cursor at the desired position. Make any desired modifications to the existing value such as inserting or deleting digits.

  6. To undo a modification of a given cell before you have committed it, press Escape. To commit a modification, press Enter, Tab, or Shift-Tab to move to the next cell, or simply select on another cell.

1. If you have multiple x-axes or y-axes in an XY line plot, the variables assigned to the x and y-axis in the first available mapping will be used.
2. Use the $!INTERFACE DATA {DERIVATIVEBOUNDARY = method} setting the configuration file tecplot.cfg to select the method to use. Set method to SIMPLE or COMPLEX.