A spline is a mathematical function defined to link a specified set of points with a function that is continuous and smooth (differentiable) at every point. The most common type of spline, the cubic spline, is defined using a set of cubic polynomials, one for each interval between the data points.
Splines can be natural or clamped: natural splines are twice-differentiable at the end points and the second derivative is zero at those points, while clamped splines have known first-derivatives at the boundary points. Before plotting the spline, the data points are sorted in increasing value along the independent axis.
|
|
The Sort option of the Definitions page of the To fit a spline function to your data, right-click in the Curve Type column on the Curves page of the Mapping Style dialog and select "Spline." By default, this option fits a natural cubic spline.
To specify a clamped spline:
1.Right-click in the Curve Setting column on the Curves page of the Mapping Style dialog and choose Settings.
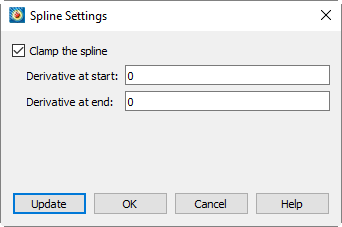
2.In the Spline Settings dialog (shown below), select "Clamp the Spline", and enter values for the derivative at the start and end of the spline.
