Whereas massless particles always travel with the local fluid velocity, particles with mass travel according to a more complicated equation of motion where the fluid creates drag on the particle. In addition, particles with mass may have a temperature that is different from the local fluid temperature, and they may lose mass due to ablative processes such as vaporization. The Particle Mass Options dialog allows you to enter coefficients and particle properties to indicate how these mass-related effects are calculated.
The Particle Mass Options dialog is displayed by selecting Mass Options on the Particle Paths and Streaklines dialog. It allows you to specify either general or detailed coefficients related to the particle trajectory and heat transfer calculations, plus options related to gravity and the initial particle velocity. If you choose to calculate the particle temperature, you may choose to terminate the particle at a specified temperature, or, with the detailed coefficient option, to ablate the particles until their mass reaches zero.
Selecting a Coefficient Set
You may enter either general coefficients or detailed coefficients. General coefficients are a convenient way of characterizing the particles, but result in less accurate calculations. They should only be used when the particle drag coefficient and heat transfer coefficient (if particle temperature is being calculated) are essentially constant. Detailed coefficients result in more accurate calculations, and should be used whenever the drag coefficient or heat transfer coefficient may not be constant, such as when the particle Reynolds number is less than 1000 (see page 367 for a definition of particle Reynolds number). In addition, if you wish to calculate particle ablation, you must specify detailed coefficients. Indicate your choice of coefficients by making the appropriate selection in the option box at the top of the Particle Mass Options dialog.
Calculating Particle Temperature
If you wish to calculate each particle's temperature along its path, set the Calculate Particle Temperature option. Particles begin with their temperature equal to the local fluid temperature at their insertion point (the beginning of each streamtrace you have placed). If you have chosen to enter general coefficients, enter the Temperature Time Constant in the General Coefficients section of the dialog. Otherwise, enter the specific heat (per unit mass) and the Nusselt number in the Detailed Coefficients section of the dialog. Also, select from the available options in the Termination Options section of the dialog. All of these options are discussed below.
Specifying the Effects of Gravity and Buoyancy
If you wish to include the effects of gravity in your calculation, enter the value in the gravity field and select the axis direction in which gravity acts.
If you choose the detailed coefficient set and non-zero gravity, the effects of buoyancy will also be included. Buoyancy acts in the opposite direction of gravity. It is included by subtracting from the particle mass the mass of the fluid it displaces, and multiplying the result by the gravitational constant to calculate the force due to gravity.
Buoyancy effects are not included if you choose the general coefficient set because the particle size is not specified. In this case, the value for gravity is simply added to the particle acceleration that is calculated from the general coefficients and local flow conditions.
Specifying the Initial Particle Velocity
Each particle injected into the flow begins either at the velocity of the flow at the point where the particle is injected, or at zero velocity or at a specified velocity. Select one of these options from the drop-down menu and, if you have chosen Specified Velocity, enter the U, V, and W velocities.
General Coefficients
Figure 21-20 shows the Particle Mass Options dialog with the general coefficients displayed. The General Coefficients consist of the Ballistic Coefficient and, if you are calculating particle temperature, the Temperature Time Constant.
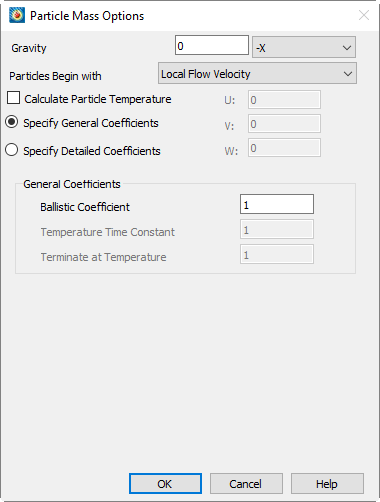
Figure 21-20. The Particle Mass Options dialog with general coefficients.
The Ballistic Coefficient is defined by the following:
where B is the Ballistic Coefficient, S is the frontal area of the particle, CD is the particle's drag coefficient and mP is the particle's mass. Given the Ballistic Coefficient, the acceleration of a particle due to fluid drag is calculated from
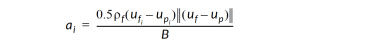
where a is particle acceleration, i stands for each spatial dimension, rf is the local fluid density 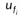and 
and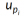 
are the velocity components of the fluid and the particle. If non-zero gravity has been specified, the acceleration in the specified direction is augmented by the value for gravity. For example, if a gravitational constant, gc, acts in the -Z direction, the acceleration in the Z direction becomes:
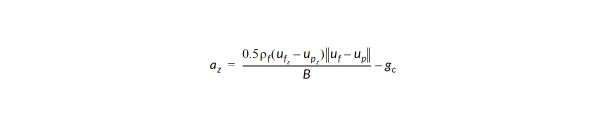
Temperature Time Constant
For the general coefficient option, particle temperature is calculated with a simple relaxation:
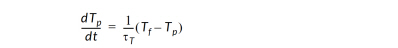
where T is temperature, and tT is the Temperature Time Constant you enter in this text field. tT has units of time, and indicates the "e-folding" time of this relaxation—the amount of time it takes to reduce the difference between the fluid temperature and the particle temperature by a factor of about 2.7.
Comparing with the convective heat transfer equation,
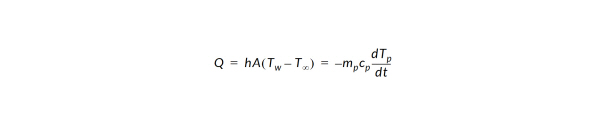
we see that tT may be thought of as a combination of the convective heat transfer coefficient, h and the surface area, mass, and specific heat of the particle:
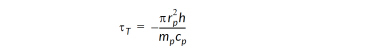
Note from that the Temperature Time Constant is only constant if the heat transfer coefficient is also constant. In general, however, this coefficient will vary with the particle's velocity relative to the fluid, so this approximation should be viewed with skepticism.
Detailed Coefficients
Figure 21-21 shows the Particle Mass Options dialog with detailed coefficients displayed. The detailed coefficients consist of particle mass radius and drag coefficient. In addition, if particle temperature is being calculated, the detailed coefficients consist of particle specific heat and Nusselt number.
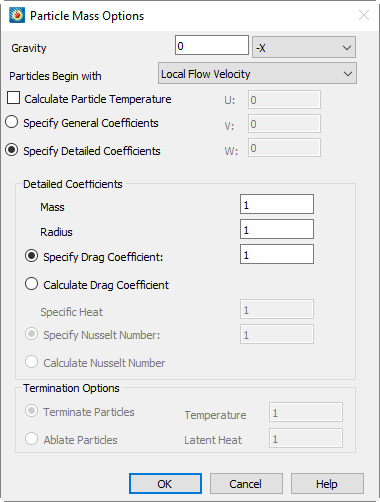
Figure 21-21. The Particle Mass Options dialog with detailed coefficients.
• Mass - Each particle begins with the same mass, entered in this text field. If ablation is being calculated, the particle's mass may be reduced by the ablative process as it travels through the flow field.
• Radius - As with Mass, each particle begins with the same radius, entered in this text field and may be reduced by ablation.
• Specify/Calculate Drag Coefficient - You may elect to specify a constant drag coefficient or have Tecplot 360 EX calculate it. If you specify a constant drag coefficient, enter its value in the corresponding text field. For calculated drag coefficient, Tecplot 360 EX uses a formula from Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions (D. Gidaspow, 1994):
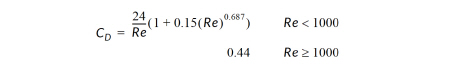
with the particle Reynolds number:
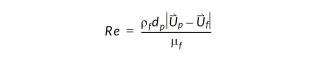
where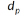 
is the particle diameter, 
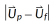is the speed of the particle relative to the fluid and 
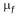is the dynamic viscosity of the gas. The acceleration then becomes:
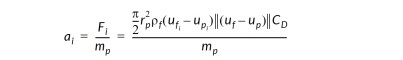
If non-zero gravity has been specified, the acceleration in the specified direction is augmented by the gravitational constant adjusted for buoyancy. For example, if a gravitational constant, gc, acts in the Z direction, the acceleration in the Z direction becomes:
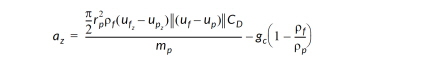
where rp is the density of the particle.
• Specific Heat - If particle temperature is being calculated, enter the specific heat per unit mass of the particles, in units of energy per mass per degree.
• Specify/Calculate Nusselt Number - The Nusselt number is a non-dimensional measure of heat transfer. The temperature change of the particle is calculated from this number using the following formula:
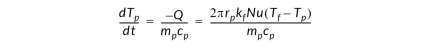
where kf is the conductivity of the fluid.
If you specify a constant Nusselt number, enter its value in the text field. Otherwise, Tecplot 360 EX will calculate it using a formula from An Eulerian-Lagrangian Analysis for Rocket Motor Internal Flows (Jayant S. Sabnis, et al., 1989):
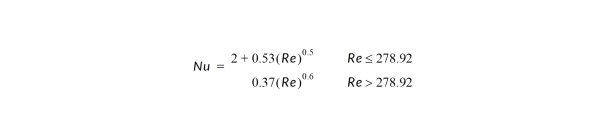
Termination Options
When solving for particle temperature, you may terminate particles when they reach a specified temperature, or calculate particle ablation (mass reduction due to off-gassing or some sort of sloughing of material from the particle).
• Terminate/Ablate Particles - If you elect to terminate the particles at a particular temperature, you must enter the temperature. When the particle reaches this temperature, its path will be terminated at that location. If you elect ablation, you must enter the temperature at which ablation begins, and the latent heat of the ablative process. If you wish to model boiling of initially solid particles, enter the latent heat of fusion plus the latent heat of vaporization, as a positive number. Once the particle reaches the specified temperature, any additional heat transferred to the particle will result in ablation instead of an additional temperature rise. If the particle's mass reaches zero, it will be terminated at that location.
• Temperature - For temperature-based termination, this is the temperature in absolute units at which the particle will be terminated. For ablation, this is the temperature at which the ablation begins.
• Latent Heat - This is the combined latent heat of fusion and vaporization for the particle, used only for particle ablation. Its units are energy per unit mass.